در این مقاله رگرسیون خطی ساده در stata را به صورت گام به گام با هم مرور می کنیم.
به طور کلی ما دو نوع رگرسیون خطی داریم، رگرسیون خطی ساده و رگرسیون خطی چندگانه
در رگرسیون خطی ساده فقط یک متغیر مستقل داریم و در رگرسیون خطی چندگانه بیش از یک متغیر مستقل داریم.
برای شروع کار با استاتا، ابتدا داده ها را وارد نرم افزار می کنیم. در این مقاله آموزشی ما دو مجموعه داده فرضی را آماده کرده ایم. داده ها را دانلود و در یک مسیر مشخص در کامپیوترتان ذخیره کنید.
برای انجام رگرسیون خطی در استاتا stata، چند گام را باید طی کنیم که در ادامه به صورت مفصل به آن می پردازیم.
گام اول: وارد کردن داده ها در stata
برای وارد کردن داده ها به نرم افزار استاتا راه های مختلفی وجود دارد. اینجا چون داده های ما به صورت فایل excel هستند ما از مسیر File>Import>Excel Spreadsheet داده ها را وارد نرم افزار می کنیم.
بعدا از انتخاب نوع فایل excel و یافتن مسیر داده ها در کامپیوتر از طریق دکمه brows، داده های ما در قسمت preview نمایش داده می شوند، بالای این قسمت دو گزینه وجود دارد، گزینه اول Import first row as variable را اگر تیک بزنیم داده ها با نام متغیر وارد نرم افزار می شوند. گزینه دوم هم بدون نام است.
بعد از وارد کردن داده ها به نرم افزار استاتا، از قسمت (Edit)Data Editor یا با تایپ کلمه edit در قسمت کامند (نوارپایین در استاتا) می توانیم داده ها را مشاهده کنیم.
داده ها ممکن است به حالت عددی یا رشته ای توسط نرم افزار خوانده شده باشند، برای کا با داده ها لازم است داده هایی که ماهیت عددی دارند را به Numeric تبدیک کنیم. برای انجام این کار در قسمت کامند stata کد زیر را تایپ و اجرا می کنیم.
destring income happiness, replace
اکنون می توانیم با استفاده از دستور summarize خلاصه ای از داده ها را ببینیم. این جدل شامل تعداد مشاهدات، مقدار حداقل، انحراف میعار، مقدار میانگین و حداکثر می شود.

گام دوم: بررسی فروض اساسی
برای انجام رگرسیون خطی ساده در stata باید فروض اساسی از قبیل استقلال مشاهدات، نرمال بودن توزیع داده ها، خطی بودن و عدم واریانس ناهمسانی را بررسی کنیم.
1- اسقلال مشاهدات
در مدل خطی ساده چون فقط دو متغیر داریم، نیازی به چک کردن این فرض نیست.
2- نرمال بودن توزیع داده ها
برای اینکه بدانیم داده های ما توزیع نرمال دارند یا خیر، می توانیم از رسم نمودار هیستوگرام استفاده کنیم. در قسمت کامند یا نوار پایین استاتا، دستور histogram happiness را تایپ و اجرا می کنیم.
histogram happiness , frequency normal
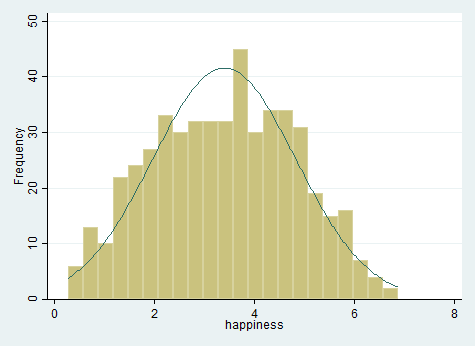
نمودار هیستوگرام بالا نشان می دهد داده های متغیر وابسته تقریبا به صورت نرمال توزیع شده اند. بنابراین می توانیم به رگرسیون خطی ادامه دهیم.
3- خطی بودن (Linearity)
برای اینکه بدانیم آیا متغیرهای ما رابطه خطی با یکدیگر دارند یا خیر، از رسم نمودار نقطه ای یا Scatter plot استفاده می کنیم. در قسمت کامند استاتا کد زیر را تایپ و اجرا می کنیم.
twoway (scatter happiness income)
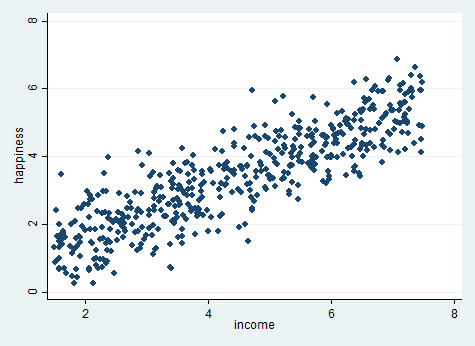
نمودار نقطه ای بالا بین متغیر شادی و درآمد نشان می دهد، یک رابطه خطی بین این دو متغیر وجود دارد. بنابراین می توانیم رگرسیون خطی را ادامه دهیم.
4- واریانس همسانی
واریانس همسانی در واقع بیانگر یک روند ثابت از خطای پیش بینی در محدوه پیش بینی مدل است. می توانیم این مورد را بعد از تخمین مدل بررسی کنیم.
گام سوم: تخمین رگرسیون خطی ساده در stata
اکنون وقت آن رسیده است که تخمین رگرسیون خطی بین دو متغیر income و happiness را انجام دهیم. در قسمت کامند stata دستور زیر را تایپ و اجرا می کنیم.
reg happiness income
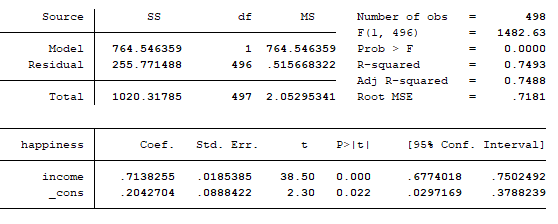
مدل برآورده شده:
happiness = 0.2042704 + 0.7138255*[income]
| Mean Square | Sum of Squares | Df | Source |
| MSS/1=764.546359 | 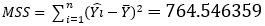 | 1 | Model “Regression” |
| 0.515668322=MSS/(n-2) | 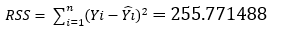 | 496=(n-2) | Residual “Error” |
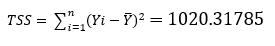 | 497=(n-1) | Total, corrected |
تفسیر اعداد و ارقام مهم رگرسیون خطی ساده در stata:
مقدار R-squared: آماره R2 مقدار توضیح دهندگی مدل را بیان می کند. به طوریکه مقدار این آماره هرچقدر نزدیک به عدد 1 باشد، یعنی متغیرهای مستقل به خوبی تاثیر عوامل موثر بر مدل را توضیح می دهند. در اینجا R2 برابر با 0.749 است که نشان می دهد متغیر incom به خوبی مدل را توضیح می دهد.
آماره Prob > F: آماره F نشان می دهد که آیا مدل ما به طور کلی به درستی تبین شده است یا خیر، هر چقدر آماره Prob > F نزدیک به عدد صفر باشد، یعنی مدل به درستی تبیین شده است.
ضرایب (coef): ضریب برآورد شده برای متغیر income تقریبا برابر با 0.71 است. یعنی با افزایش 1 واحدی در درآمد، متغیر شادی 0.71 افزایش می یابد.
آماره Std. Err: هر چقد مقدار آماره انجراف استاندارد کمتر باشد، یعنی مدل بهتری برآورد کرده ایم.
آماره t: هر چقدر آماره t بزرگتر باشد به معنی این است که مدل بهتری برآورد کرده ایم. اگرآماره t بزرگتر از 2 باشد، بیانگر معناداری متغیرهای برآورد شده در مدل است.
P>|t|: هرچقدر مقدار این آماره کمتر باشد بهتر است. یعنی مقادیر کمتر از 0.05 را به عنوان متغیرهای معنادار در مدل در نظر می گیریم. برای مقادیر بزرگتر یا باید متغیرها را از مدل حذف کنیم یا از مدل های دیگر برا تخمین متغیرها استفاده کنیم.
گام چهارم: بررسی همسانی واریانس
یکی از آزمون های مهم در رگرسیون خطی، بررسی واریانس همسانی است. در آزمون واریانس همسانی ما به دنبال بخش خطاهای مدل هستیم. یک برآورد خوب باید باقیمانده هایی با واریانس همسان داشته باشد.
برای بررسی واریانس ناهمسانی در استاتا از روش رسم نمودار residuals یا از طریق آزمون های وایت و بروش-پاگان اقداام می کنیم.
روش اول: استفاده از رسم نمودار
برای آزمون رسم نمودارهای بخش خطای مدل از طریق تایپ و اجرای کد زیر در استاتا استفاده می کنیم.
rvfplot , yline(0)
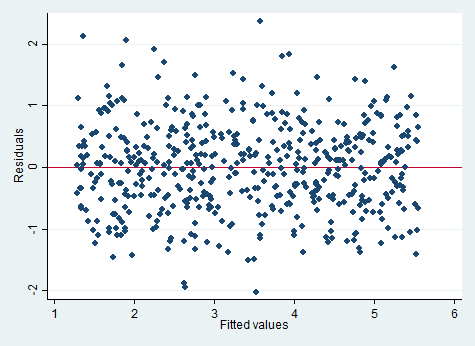
در نمودار اغلب مشاهدات باقیمانده حول محور صفر توزیع شده اند. می توانیم فرض واریانس همسانی را بپذیریم.
روش دوم: استفاده از آزمون white
از طریق تایپ و اجرای کد زیر در قسمت کامند استاتا، آزمون واریانس ناهمسانی را چک می کنیم.
estat imtest
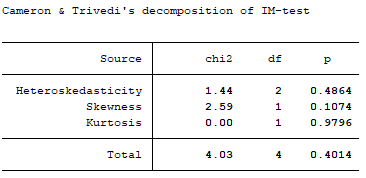
در این آزمون فرض صفر، وجود واریانس ناهمسانی در مدل است. اگر مقدار p خیلی کوچک باشد می توانیم فرض صفر (واریانس ناهمسانی) را رد کنیم. در این مدل واریانس ناهمسانی نداریم.
روش سوم استفاده از آزمون Breusch-Pagan
کد estat hettest را قسمت کامند تایپ و اجرا می کنیم.
estat hettest

در آزمون بروش-پاگان نیز فرض صفر وجود واریانس ناهمسانی است. اگر مقدار آماره Prob > chi2 کمتر از 0.05 باشد فرض صفر (وجود واریانس ناهمسانی) قبول می شود. در این مدل مقدار Prob > chi2 برابر با 0.24 است بنابراین مدل ما واریانس ناهمسانی ندارد.
گام پنجم: مصورسازی نتایج رگرسیون
برای رسم نمودار تخمین نتایج مدل در استاتا از طریق تایپ و اجرای کد زیر می توانیم اقدام کنیم.
بهتر است کدها را در یک دوفایل (dofile) تایپ کنید یا از این مقاله کپی کنید. این کار به ما کمک می کند راحتر با استاتا کار کنیم.
graph twoway (scatter happiness income , symbol(d)) (lfit happiness income ) ///
(lfitci happiness income ), title("Linear Regression Between Happiness and Income") ///
subtitle("95% Confidence Bands")
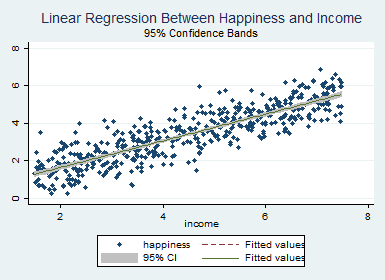
گام ششم: بررسی فروض مدل و برازش
1-تحلیل باقیمانده- بررسی نرمالیتی باقیمانده ها
با استفاده از کدهای زیر می توانیم نرمال بودن باقیمانده ها را بررسی کنیم.
predict ehat, residuals
pnorm ehat, title("Normality of Residuals of Y= happiness on X= income ")
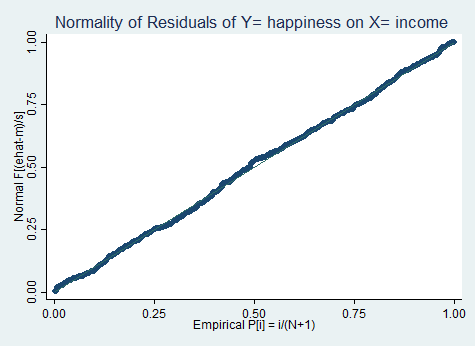
2- تحلیل باقیمانده- بررسی فاصله کوک (Cook distance)
در آزمون cook distance نباید مشاهدات باقیمانده فاصله افراطی داشته باشند.
predict cookhat, cooksd
generate id=_n
predict cookhat, cooksd
generate id=_n
graph twoway (scatter cookhat id, symbol(d)), title("Regression Between Happiness and Income") ///
subtitle("Cooks Distances")
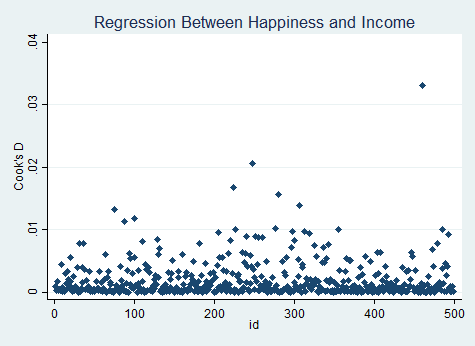
در اینجا مقدار فاصله کوک غیرمعمول وجود ندارد
3- بررسی خطی بودن باقیمانده ها
از آزمون جک نایف برای این فرض استفاده می کنیم.
predict yhat, xb
predict jack, rstudent
graph twoway (scatter jack yhat, symbol(d)), title("Regression Between Happiness and Income") ///
subtitle("Jacknife Residuals v Predicted")
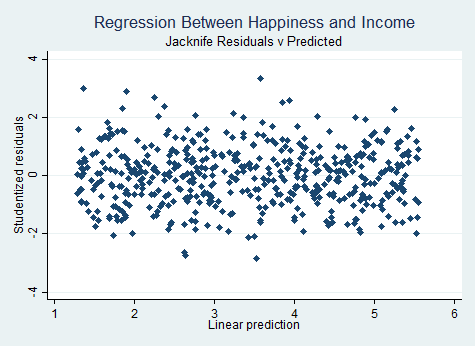
 مدرسه تخصصی اقتصاد |
مدرسه تخصصی اقتصاد |


